第七章 统计分析
前面三章介绍了DataFocus可视化视图,本章主要介绍运用视图进行统计分析的几种方法。
7.1节介绍二八法则和帕累托图的运用。
7.2节介绍如何进行平均分析,包括算数平均分析以及加权平均分析。
7.3节介绍时间序列分析相关概念。
7.4节介绍基本散点图以及高级散点图的运用。
7.5介绍常用的增速比较,包括同比、环比和定基比。
本章用到四个数据源:
“采购数据”,其中每条记录代表在一个供应商的购买金额,字段包括供应商代码、购买金额。
“学生成绩表”,其中每条记录代表一位学生的成绩,字段包括姓名、小测、期中、期末。
“客服接听数据”,其中每条记录代表一条接听记录,字段包括中心、部、班、日期、人工服务接听量等。
“销售数据”,其中每条记录代表一条订单,字段包括产品类别、区域、订单日期、销售金额等。
7.1 二八法则
意大利经济学家巴莱多在19世纪末20世纪初提出了二八定律(也称二八法则、巴莱多定律)。在二八法则中,他认为,相对少量的原因通常造成大多数的问题和缺陷,即80%的问题是由20%的原因导致的。举个例子,在现实生活中我们可以看到,超市所有商品中的20%的商品带来了当月营业额的80%的利润,所有产品中,最重要的也许只有那20%,即“至关重要的极少数”。二八法则非常适用于目前这个信息高速膨胀的互联网时代,为了能更高效合理的利用企业的渠道资源,例如时间、成本等,产生更多的利润价值和社会竞争力。
在数学上,帕累托图在概念上与二八法则有关,因此二八法则也被叫做帕累托法则。帕累托图是按照一定的类别,根据发生频率的大小顺序绘制直方图,并计算出其分类所占的比例展示比例累积和的图形。
本节我们以某企业的物料采购金额数据为例绘制一个帕累托图,从而快速定位有重要贡献的供应商。在本图中,横轴为供应商代号,纵轴为采购金额,其中柱状图显示采购金额从高到低供应商排序,折线图则表示金额累计百分比沿着横轴的变化情况。如图7-1-1所示,当累计百分比为80%时,供应商大致为6家,一共30家供应商,即该企业80%的物料采购是被20%的供应商所承担的,因此这20%的供应商是该企业的主要供应来源。
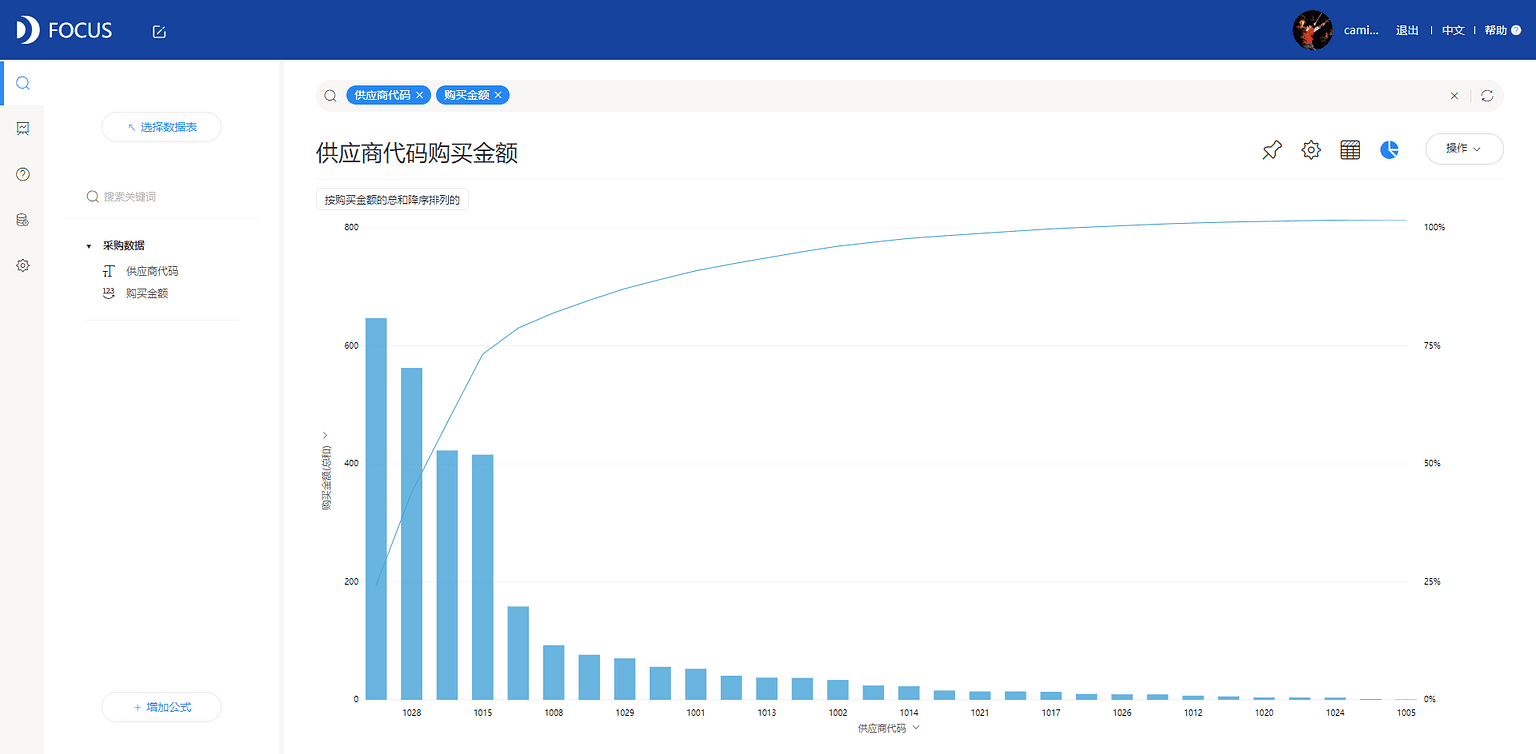
1.数据准备
导入“采购数据.xls”数据源,在本案例中需要用到的字段为“供应商代码”和“购买金额”。
2.创建帕累托图
进入搜索页面,选择数据源“采购数据.xls”。双击选择“供应商代码”、“购买金额”字段入搜索匡,系统智能呈现环图,见图7-1-2。
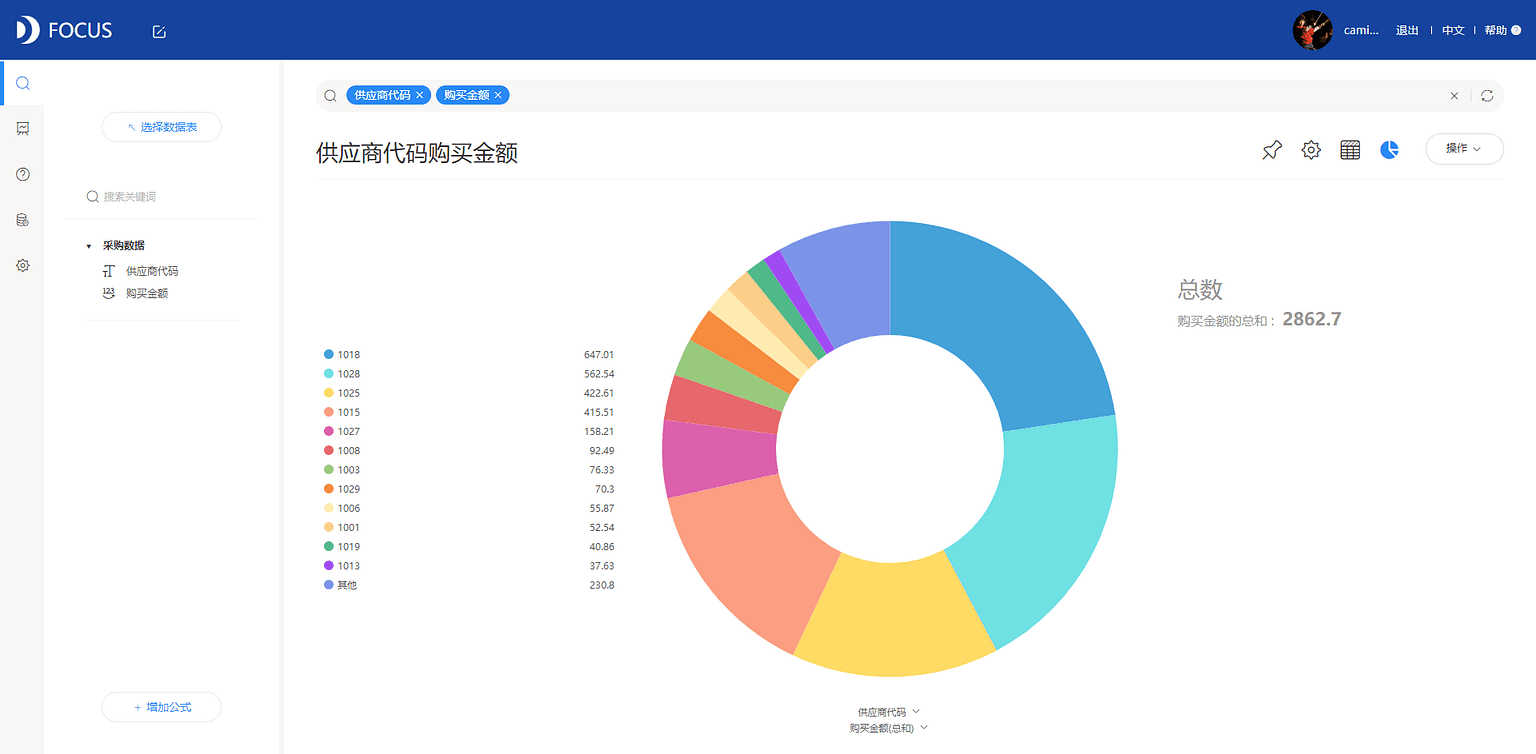
切换图形为帕累托图,见图7-1-3。
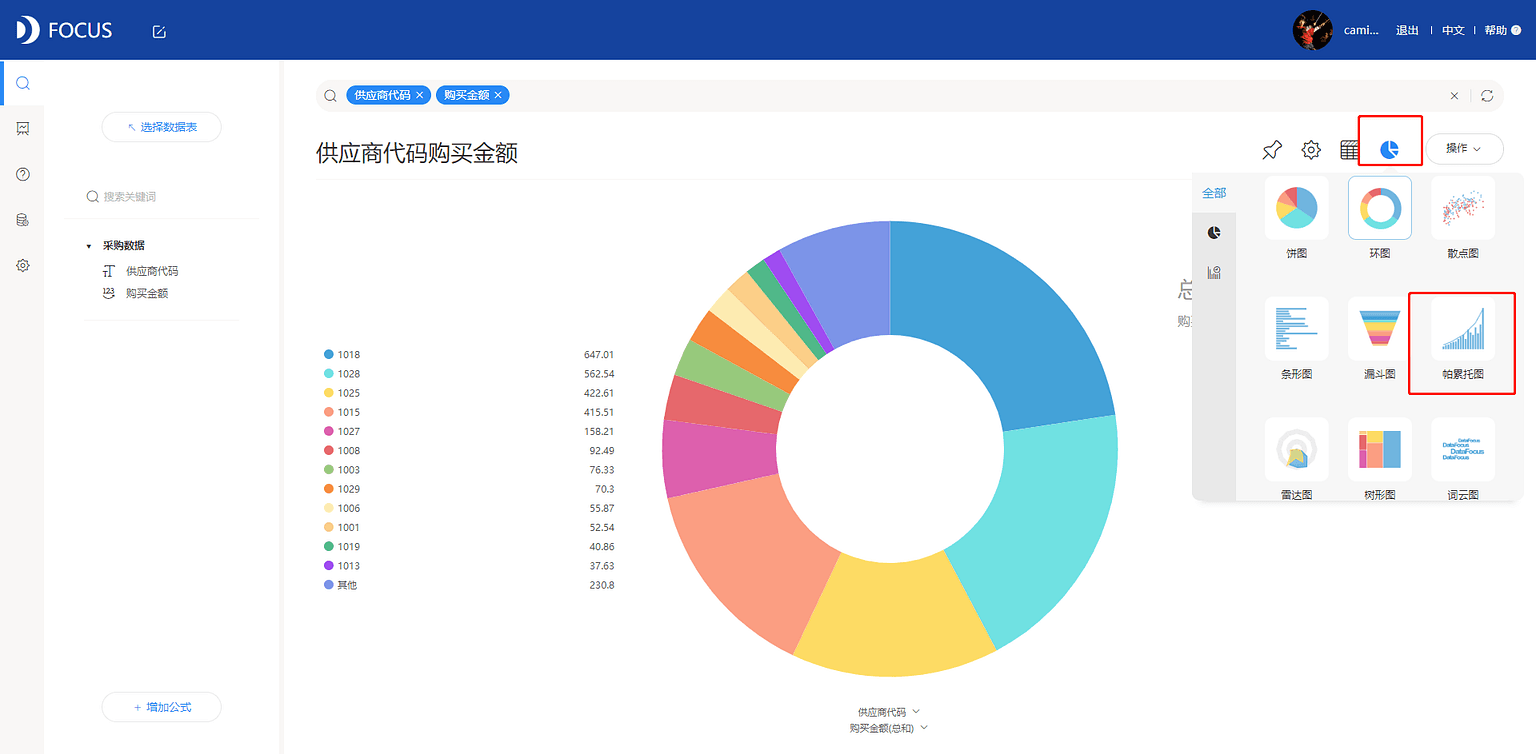
将购买金额按降序进行排序,见图7-1-4。
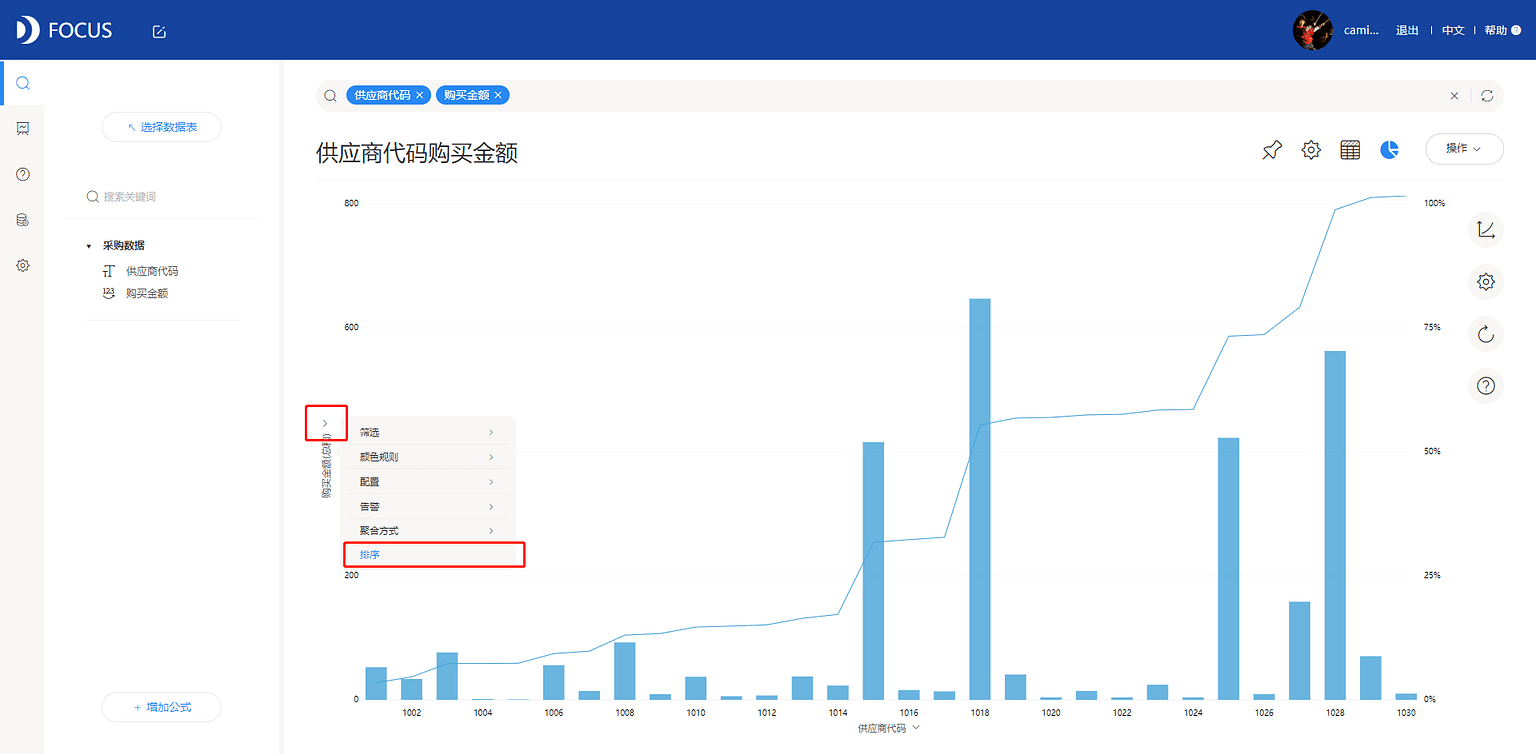
最后得到帕累托图如图7-1-5所示。

7.2 平均分析
平均分析法是通过平均数指标,反映事物目前所处的位置和发展水平。在运用平均分析法时,对不同的特征数据所采用的的平均指标有所不同,本节将举例算数平均数。算数平均数分为简单算术平均数和加权平均数。简单算数平均数即为将数据集合中所有数据之和除以数据个数;加权平均数是计算具有不同权重的数据的算数平均数。
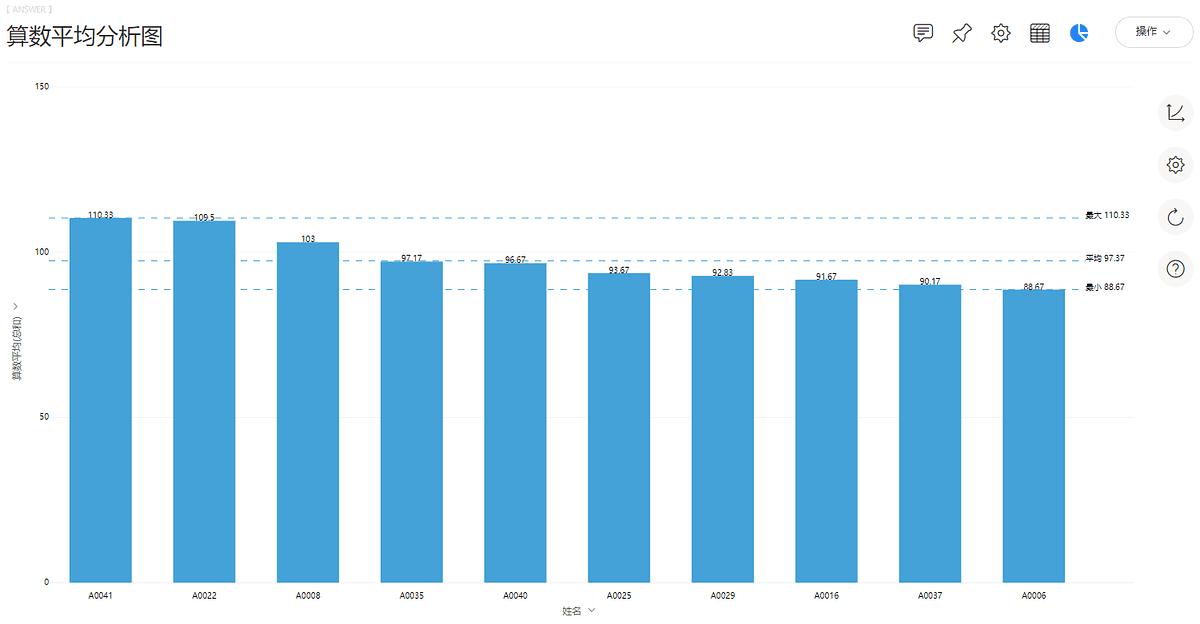
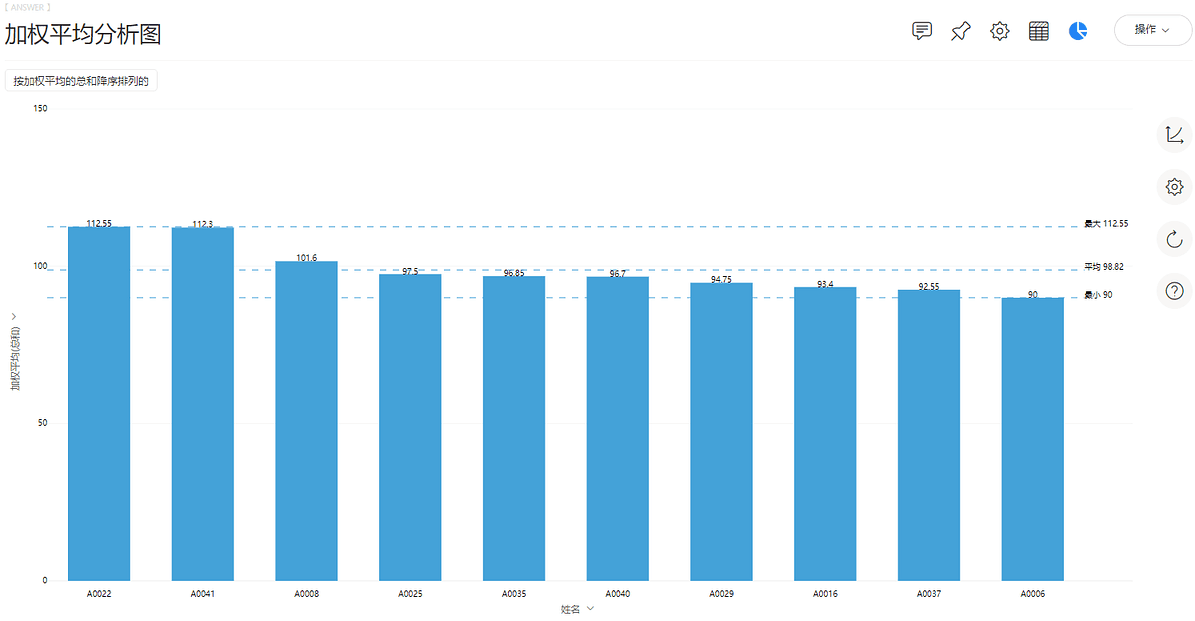
在本节中我们使用“学生成绩表”数据源,对学生的期末综合成绩进行评估。如图7-2-1和图7-2-2所示,得到两种不同平均指标下的综合成绩排名前10的学生。其中,在加权平均分析中,小测成绩权重为20%,期中成绩权重为30%,期末成绩权重为50%。
1.数据准备
导入“学生成绩.xls”数据源,在本案例中需要用到的字段为“姓名”、“小测”、“期中”、“期末”。
2.创建算数平均数视图
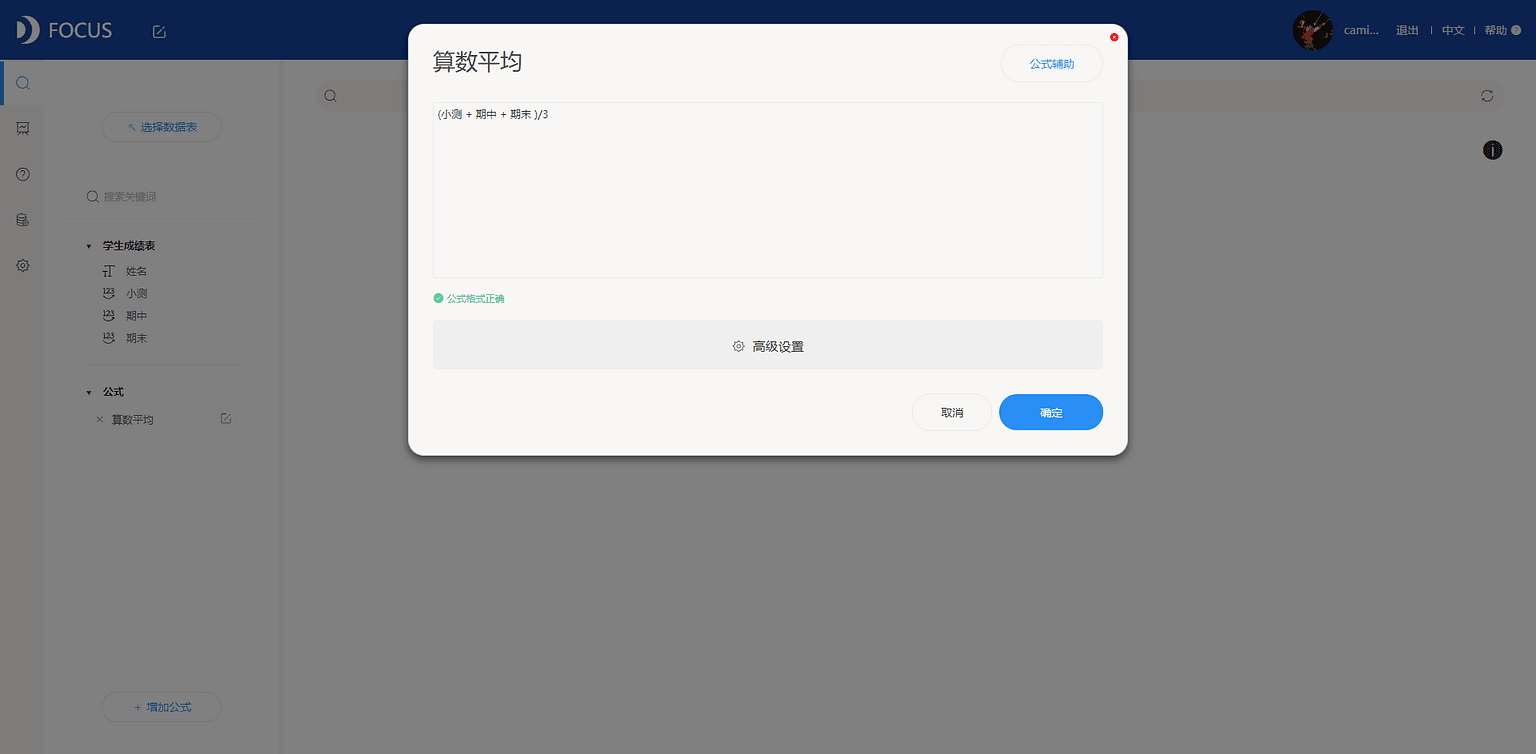
进入搜索页面,选择“学生成绩.xls”数据源。增加“算数平均”公式字段,见图7-2-3。
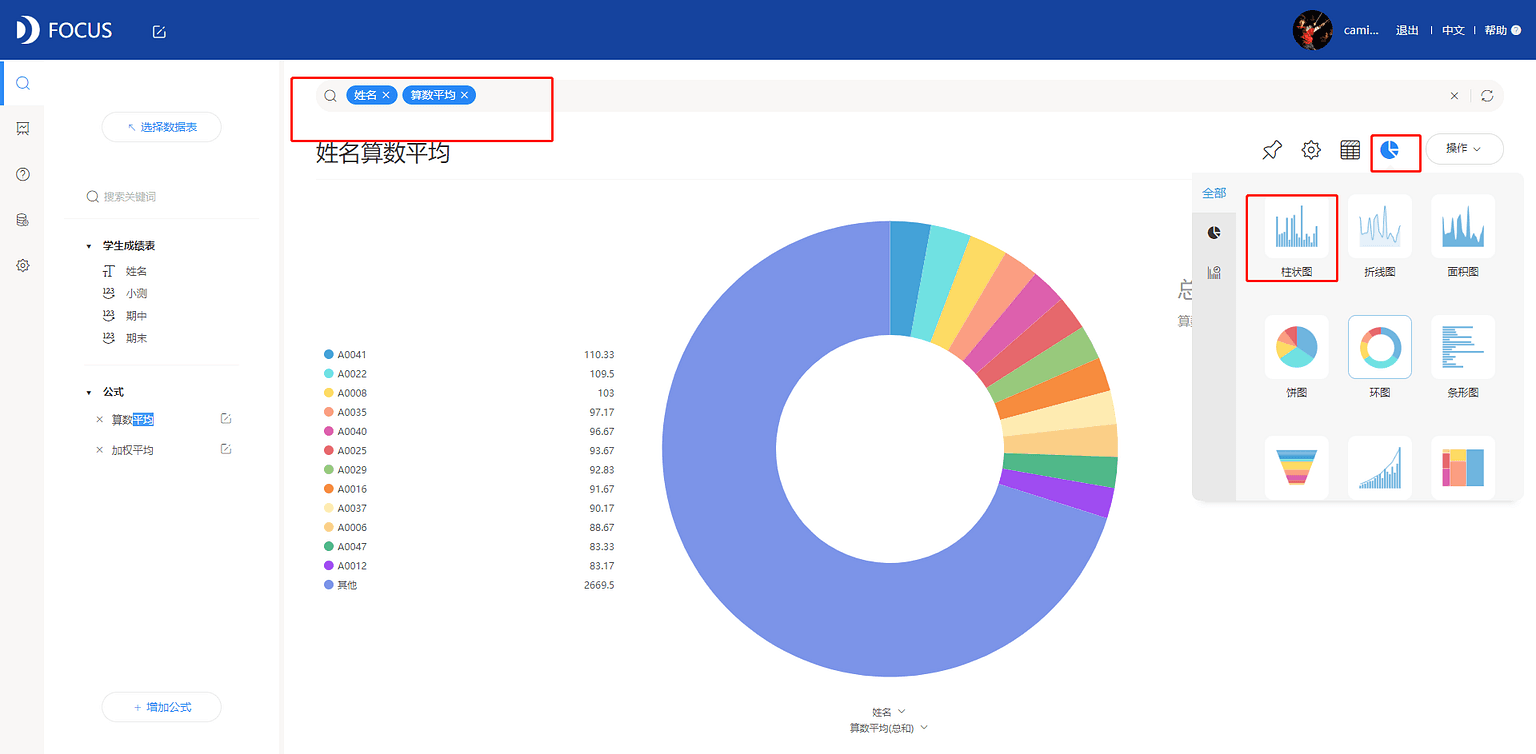
双击选择“姓名”、“算数平均”字段入搜索框,并切换图形为柱状图,见图7-2-4。
在搜索框中输入“排名前10的算数平均的总和”,筛选出综合成绩排名前10 的学生,见图7-2-5。
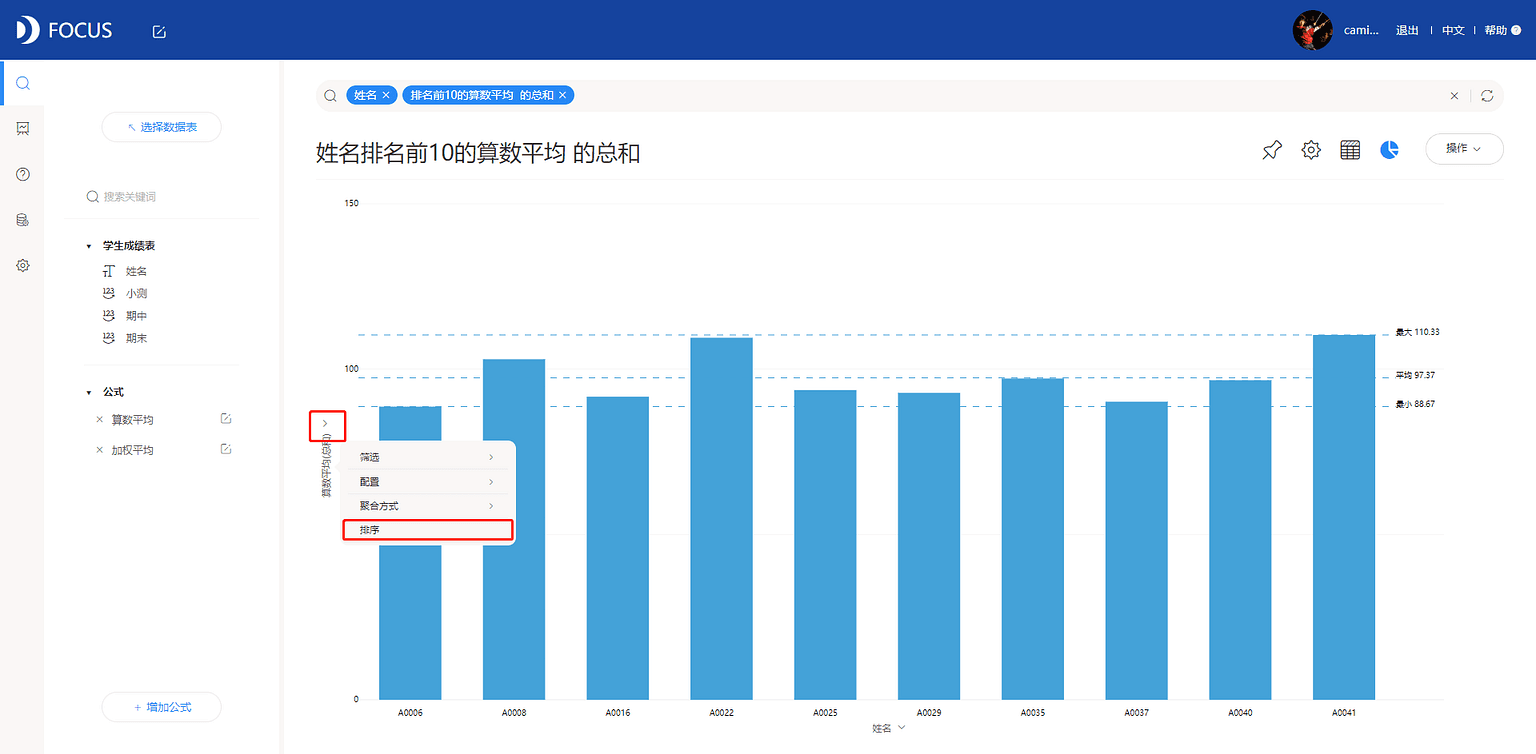
选择配置选项为显示数据标签,得到算数平均分析视图,如图7-2-6所示。
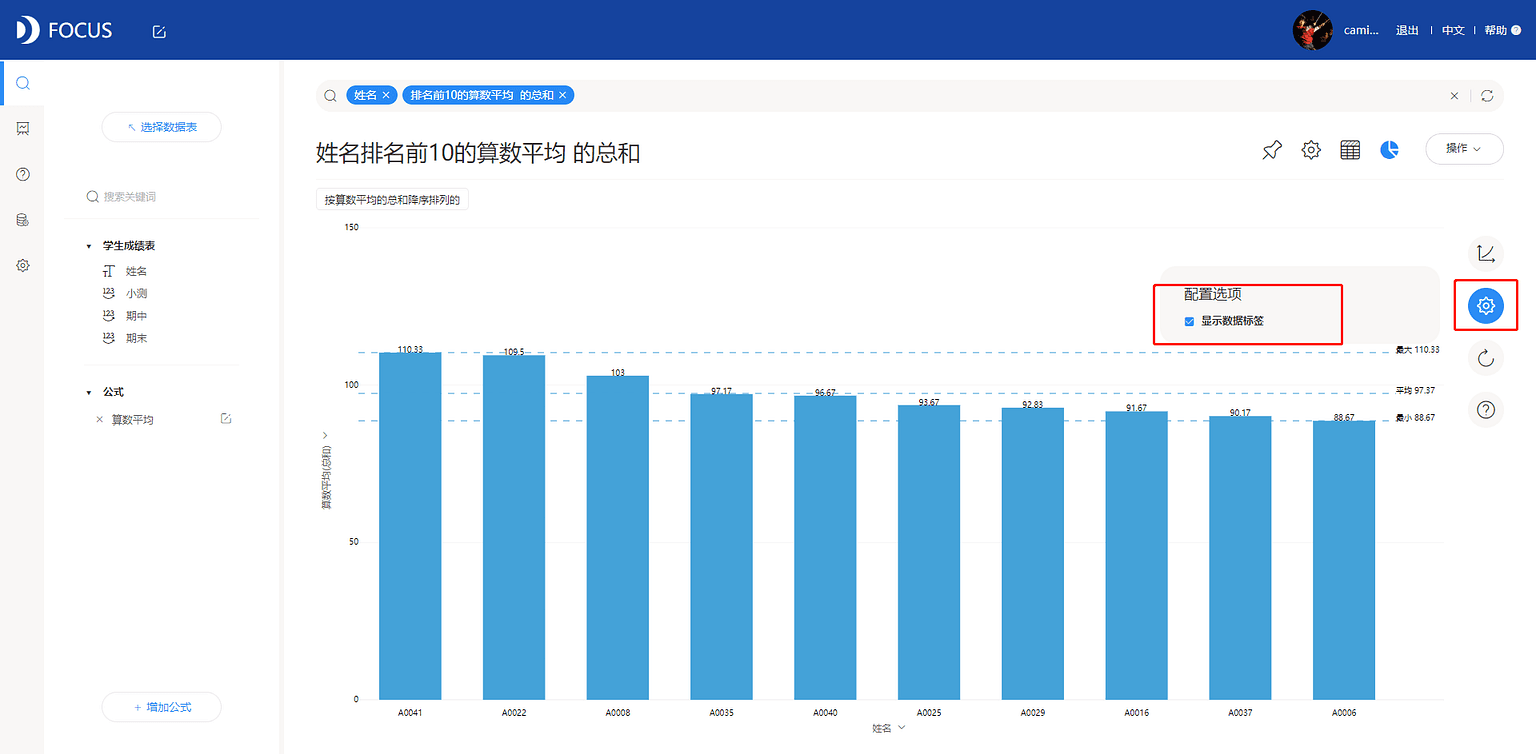
增加“加权平均”公式字段,见图7-2-7。
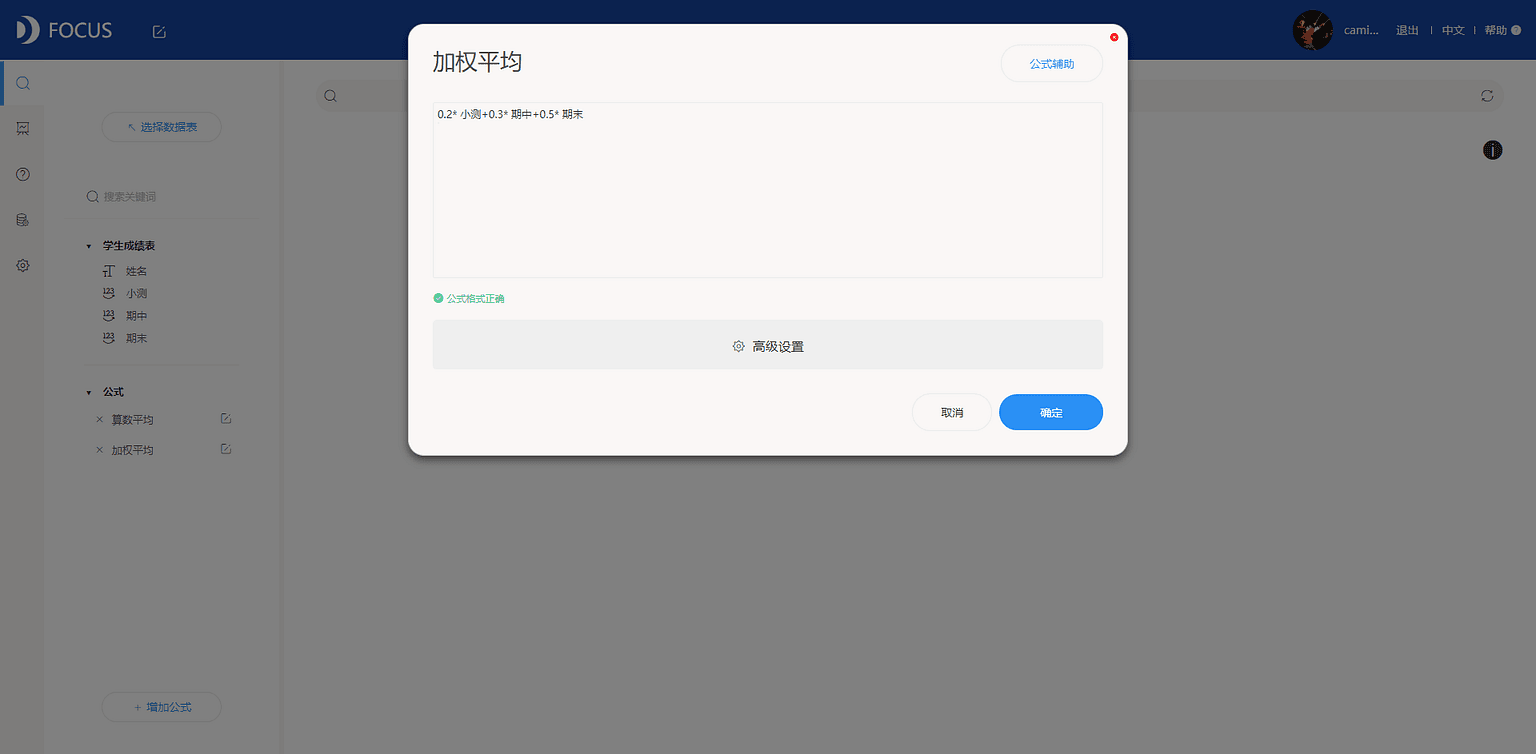
双击选择“姓名”、“加权平均”字段入搜索框,并切换图形为柱状图,见图7-2-8。
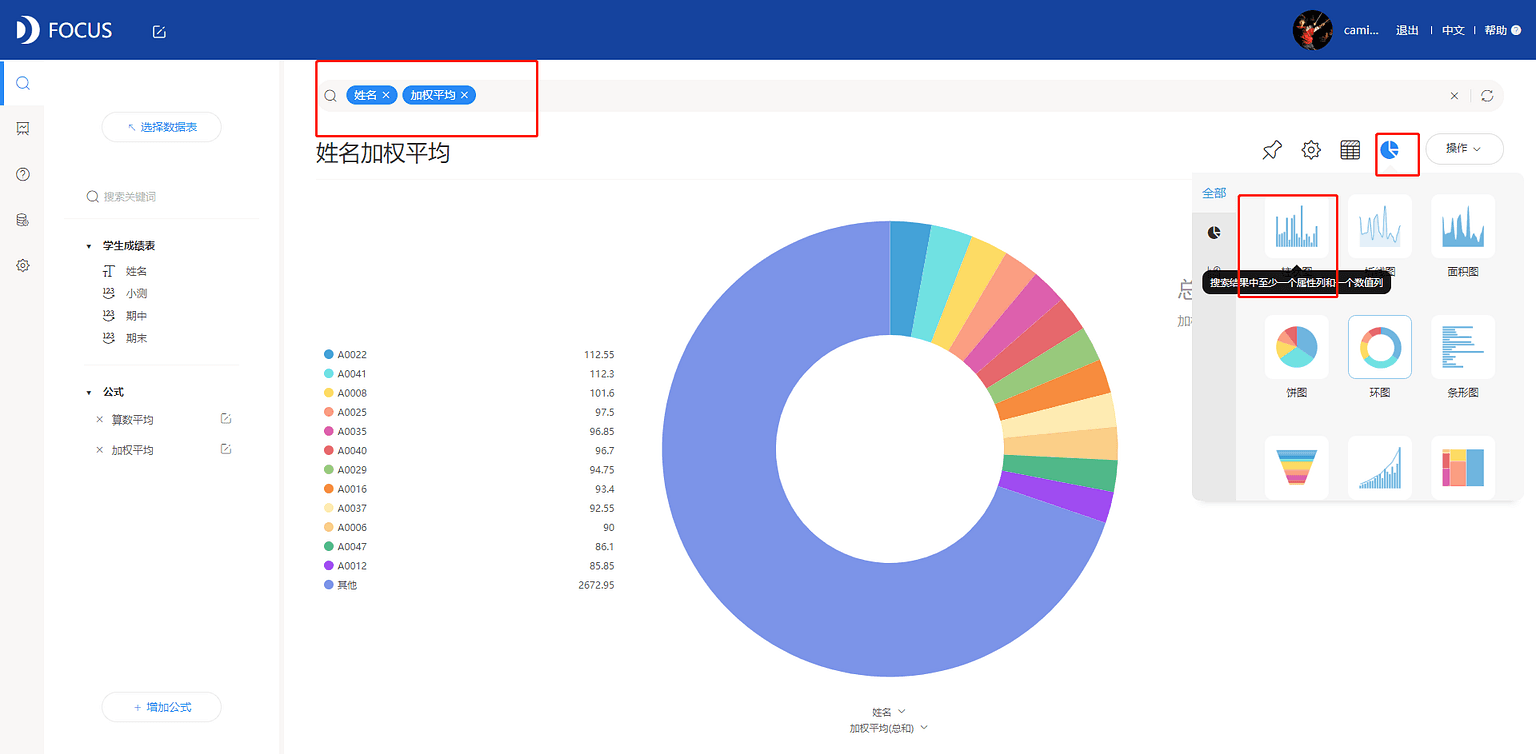
在搜索框中输入“排名前10的加权平均的总和”,筛选出综合成绩排名前10 的学生,见图7-2-9。
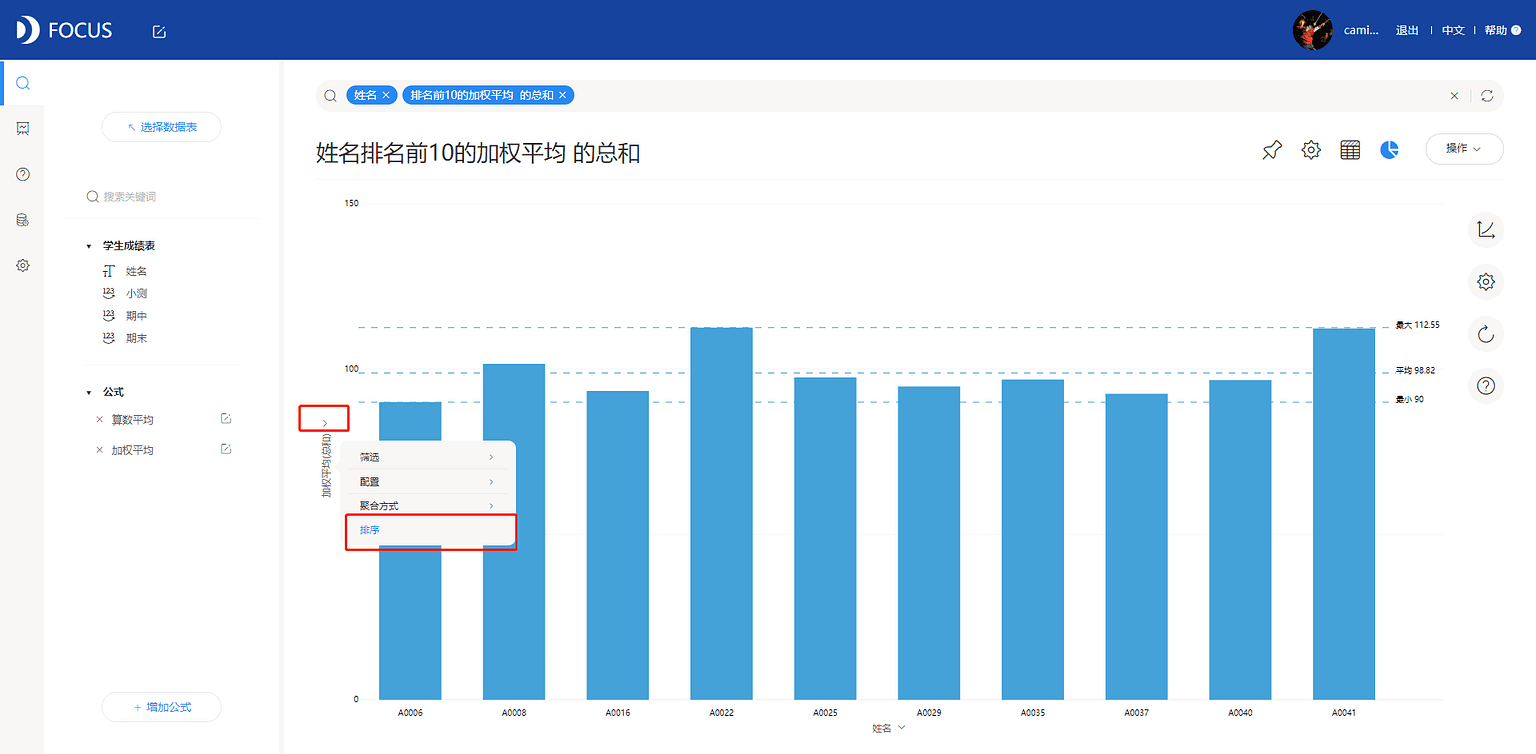
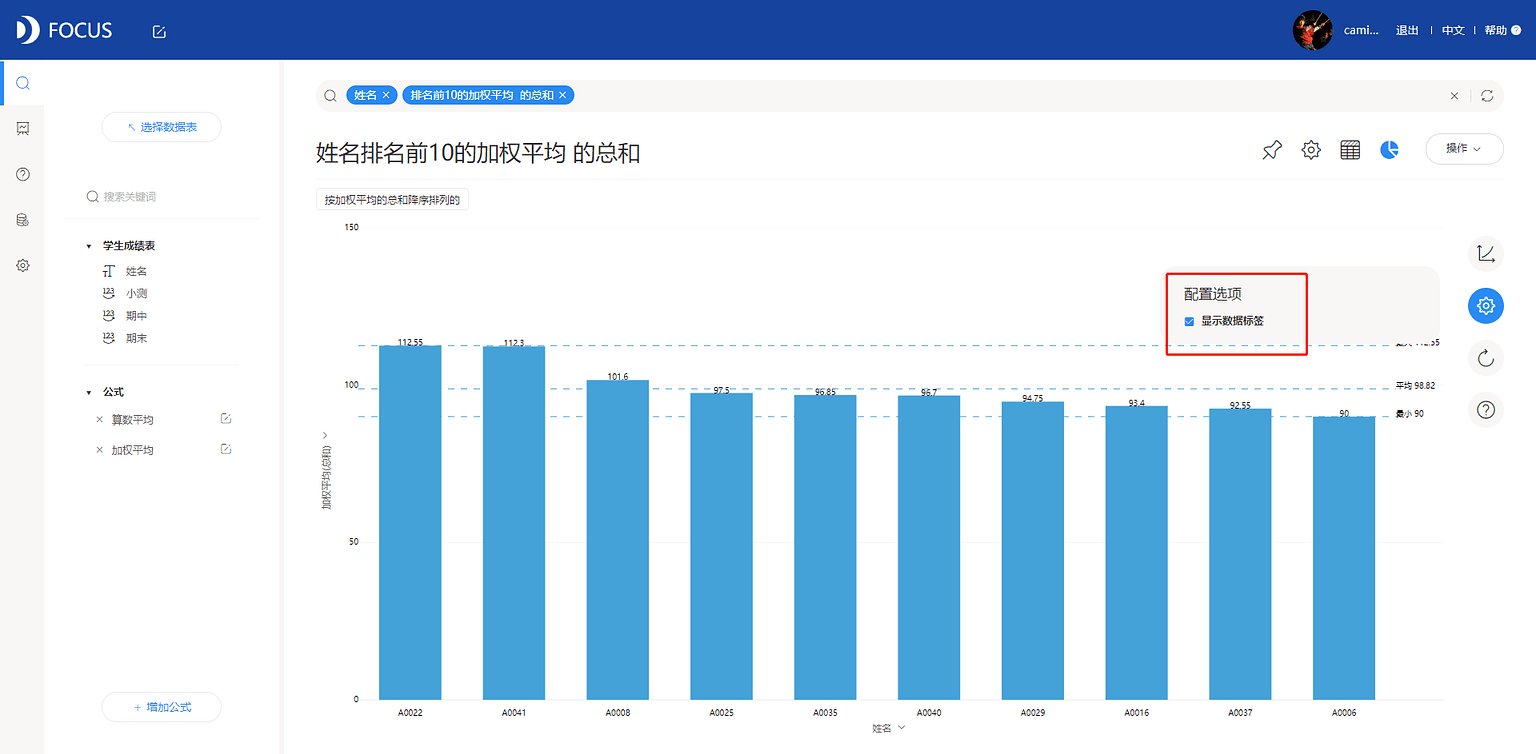
选择配置选项为显示数据标签,得到加权平均分析视图,如图7-2-10所示。
7.3 时间序列分析
时间序列分析经常应用在观察变量随时间变化的某种趋势。时间序列图以时间作为横轴,纵轴放置不同时间点上变量的取值。
下面以客服接听数据为例,创建各个部按日的人工服务接听量的时间序列图和按周的人工服务接听量的时间序列图。
(1)进入搜索页面,选择“客服接听数据”数据源。
(2)双击选择“部”、“人工服务接听量”、“日期”字段入搜索框,智能呈现折线图。
(3)适当修改主题颜色和线条粗细,见图7-3-1。
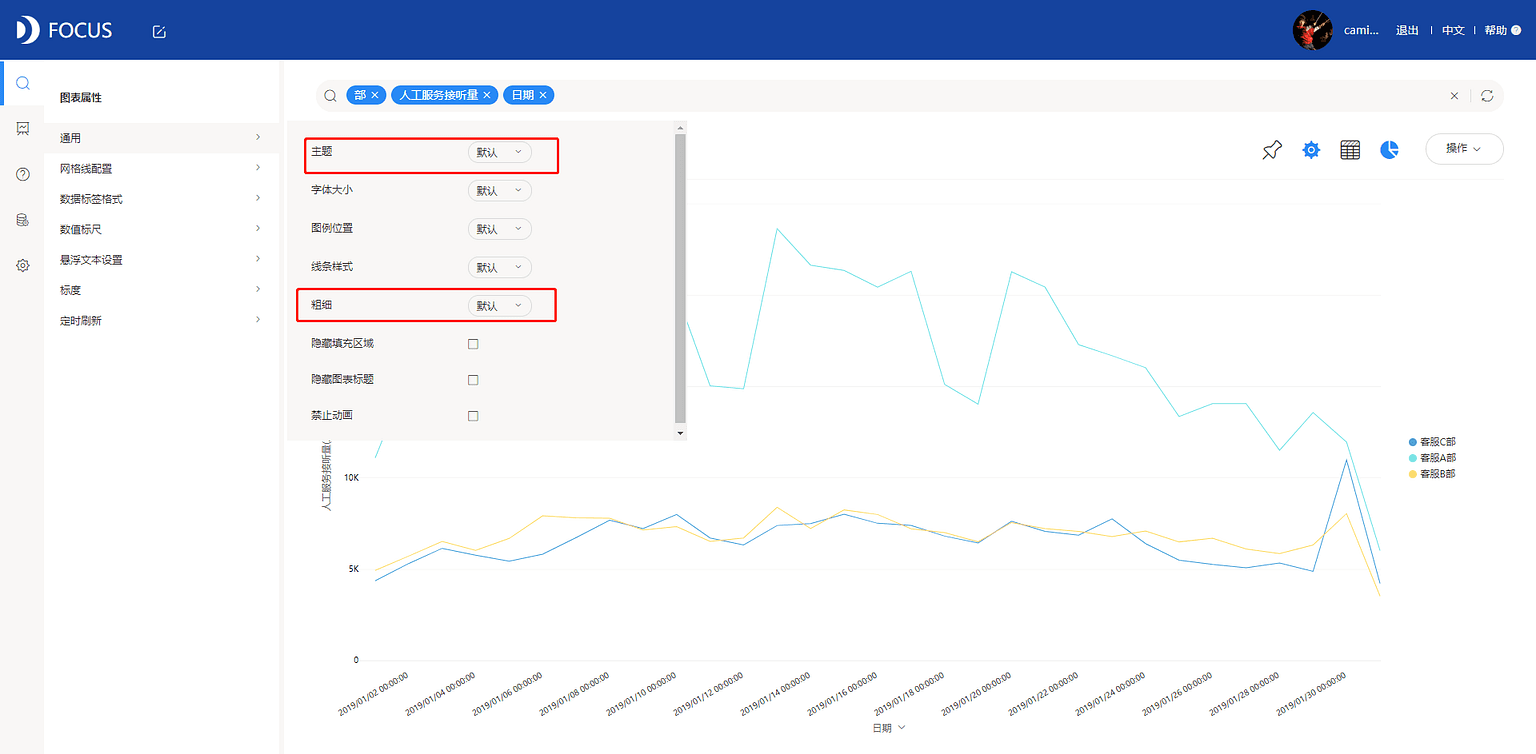
得到时间序列图如图7-3-2所示。
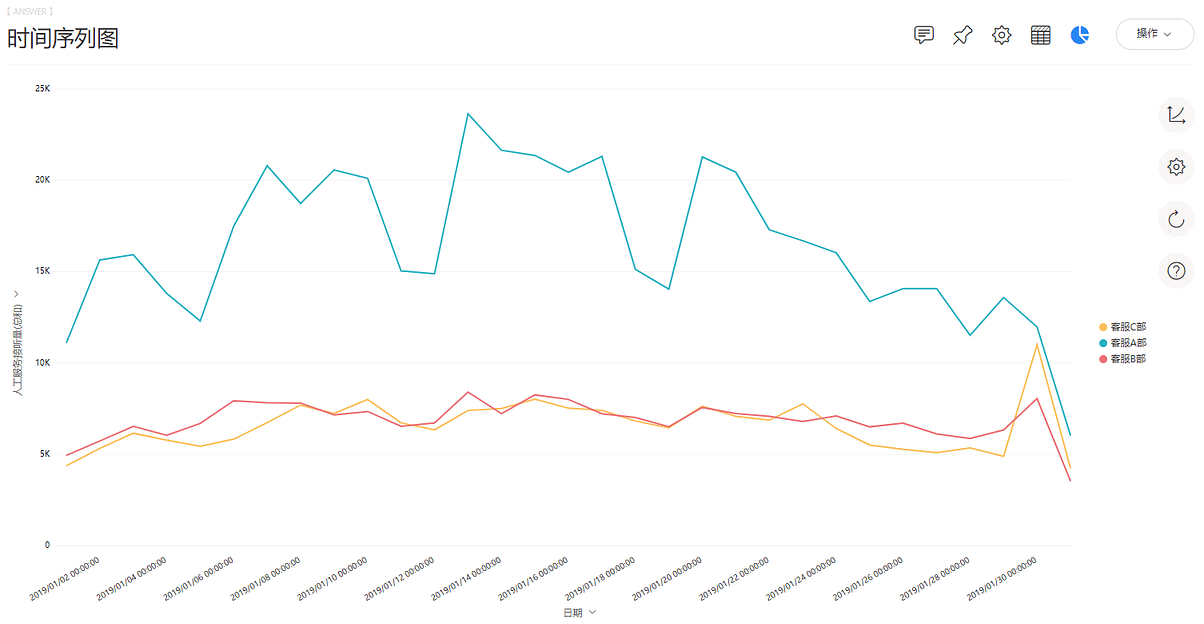
(4)如果想看按周的人工服务接听量时间趋势,可以在搜索框中输入“每周”,此时数据以周为单位统计。还可以适当修改线条样式,见图7-3-4。
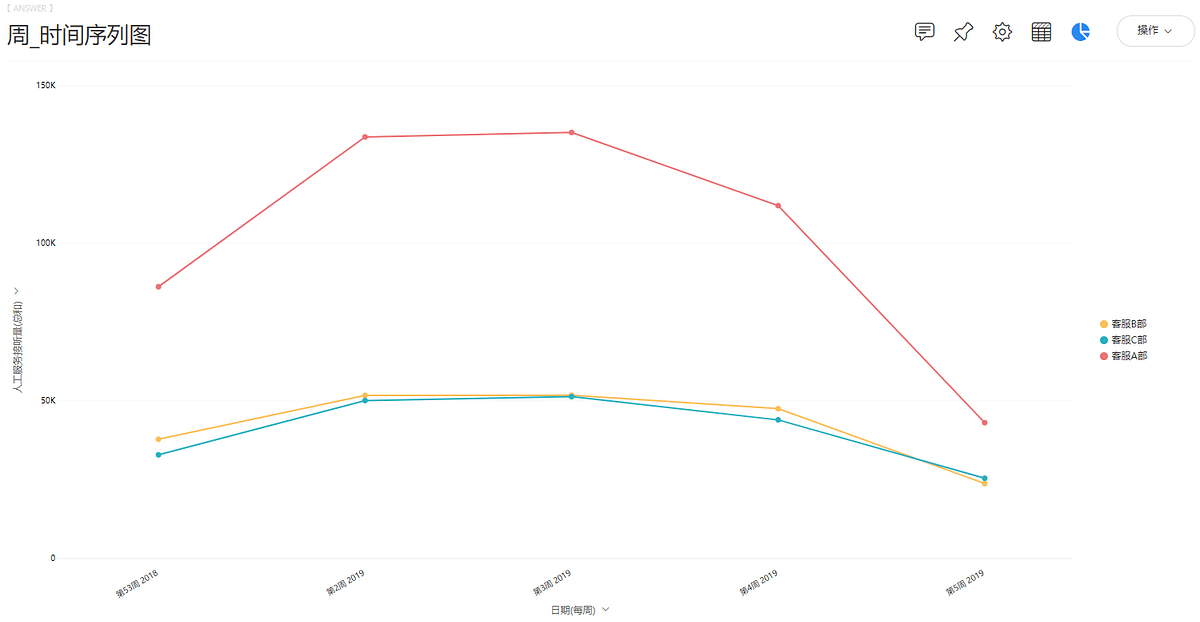
得到周_时间序列图如图7-3-5所示。
7.4 散点图与相关分析
散点图一般用于发现两个连续变量或多个变量之间的关系,通常可以通过散点图大致看出变量之间的相关关系,当存在大量数据点时结果更精准。
7.4.1创建基本散点图
本小节以客服接听数据为例,来直观展示每个班的人工服务接听量总和。
(1)选择“客服接听数据”数据源,双击选择“人工服务接听量”、“部”入搜索框,切换图形为散点图,见图7-4-1。
得到基本散点图如图7-4-2所示。
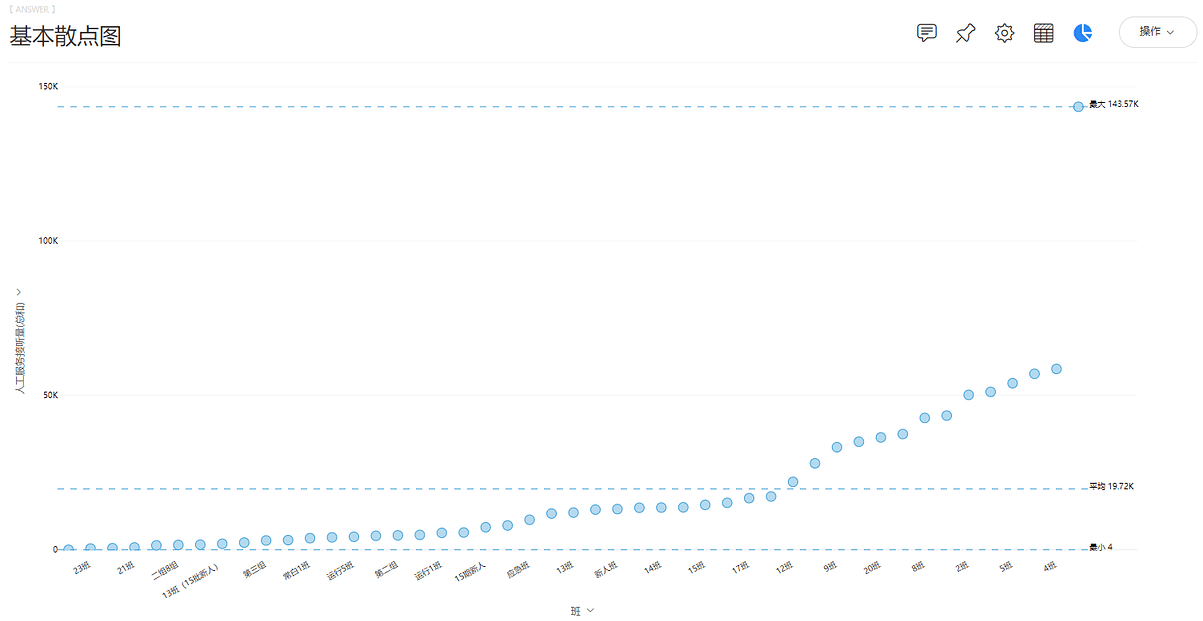
7.4.2创建高级散点图
本小节将分析人工服务接听量和平均呼入通话时长之间的关系。
(1)增加“平均呼入通话时长”字段,见图7-4-3。
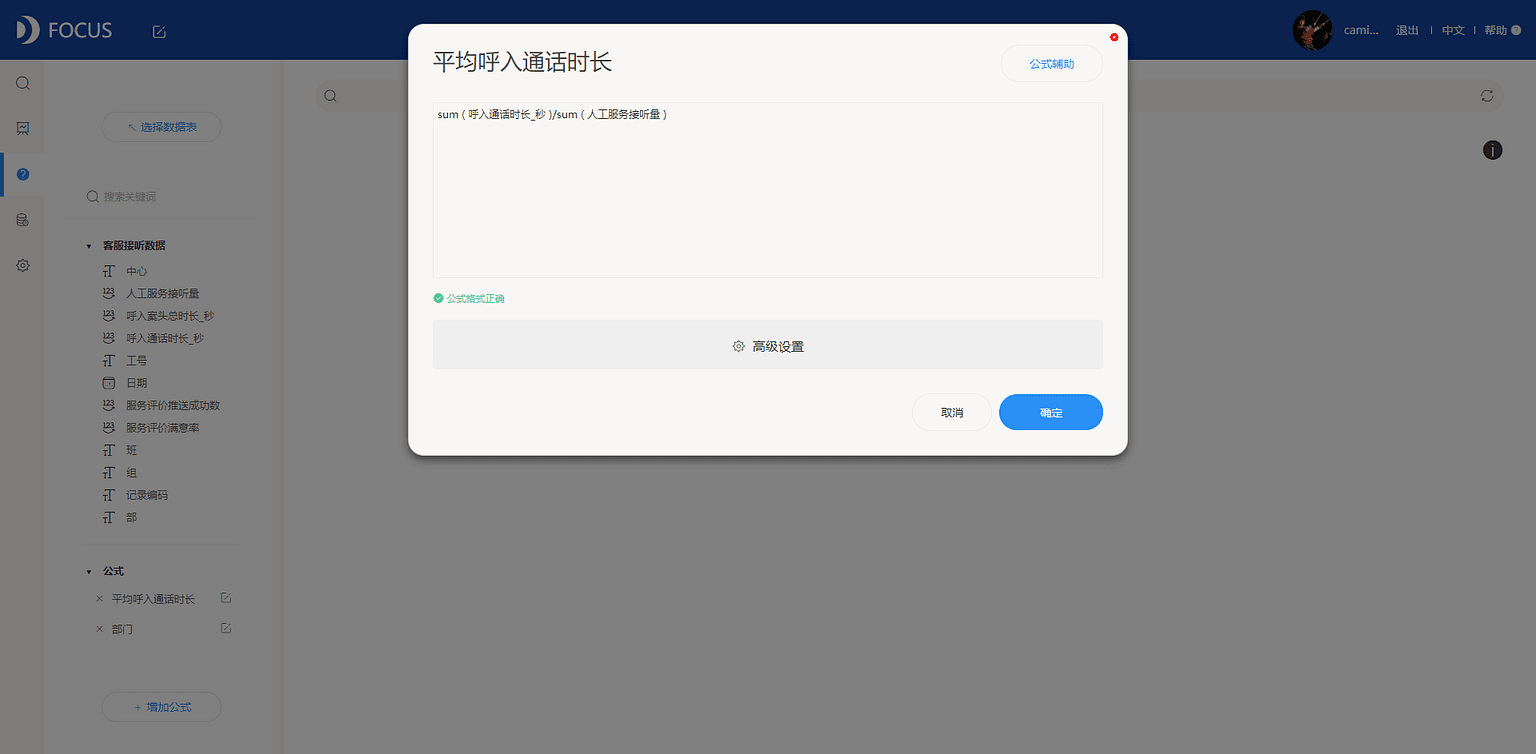
(2)增加“部门”字段,将“中心”和“部”数据列进行整合,见图7-4-4。
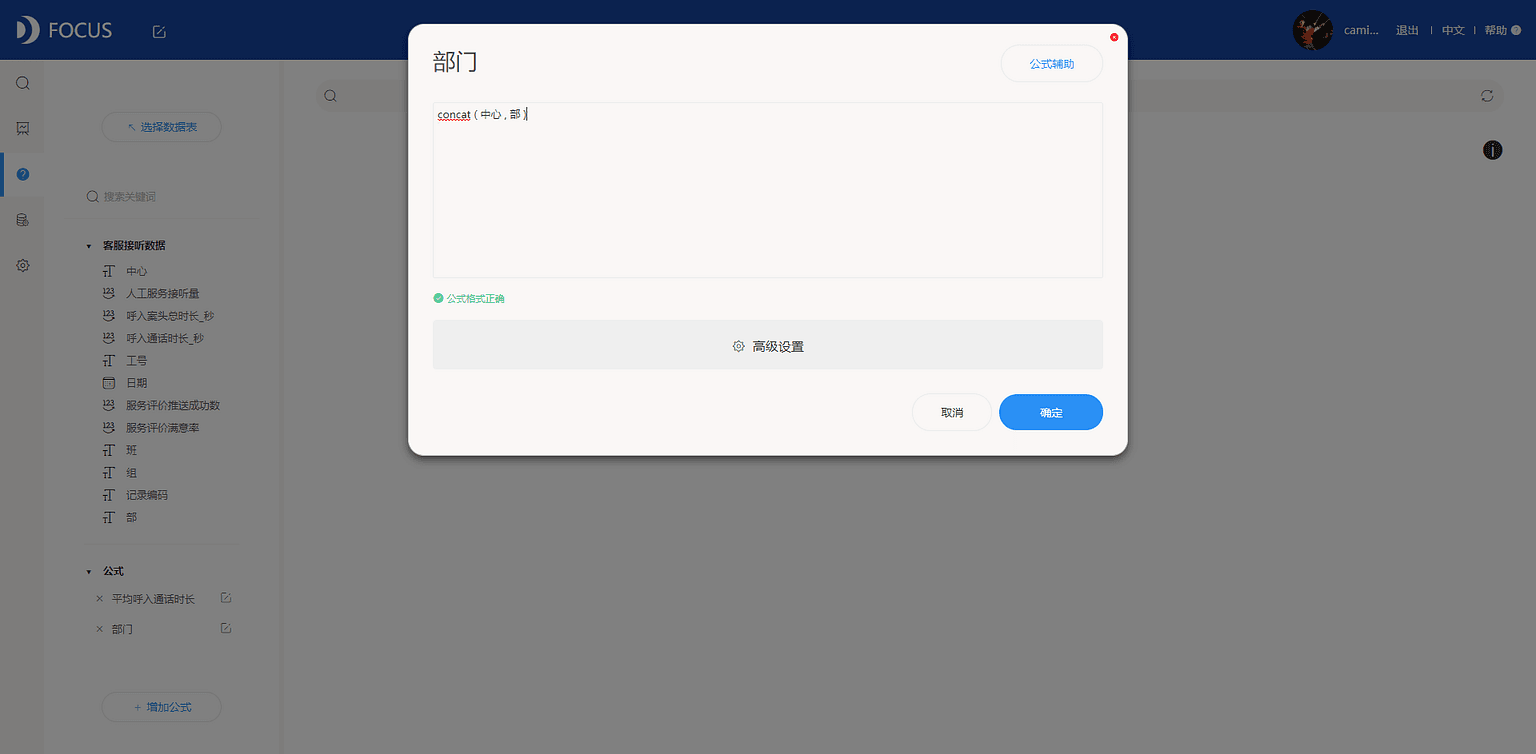
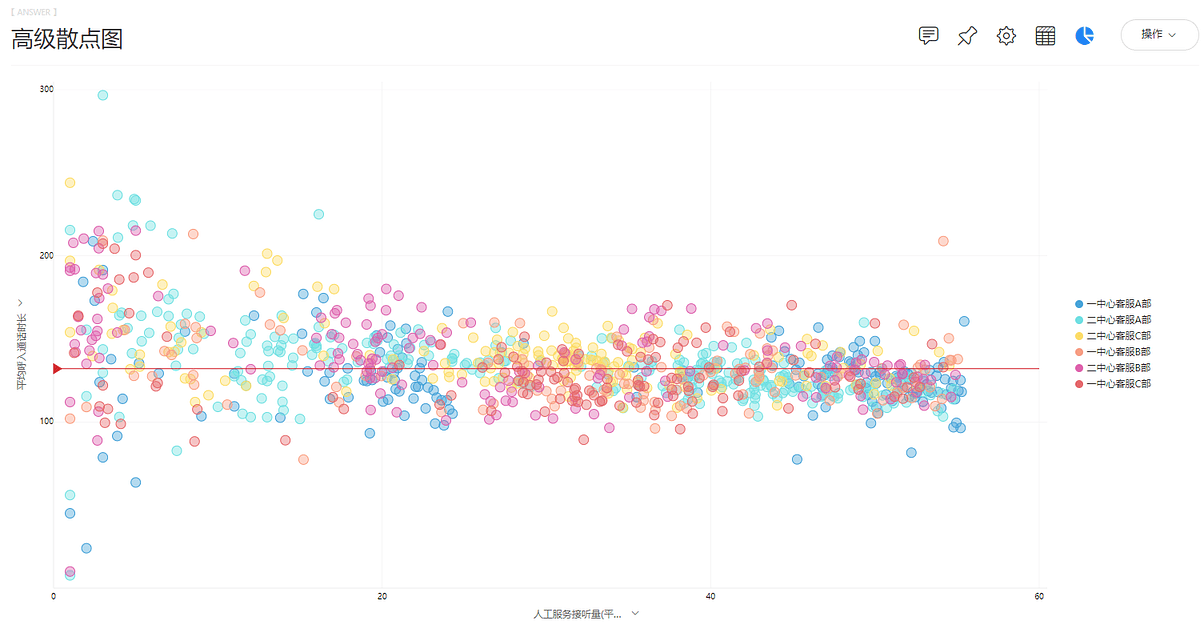
(3)双击选择“人工服务接听量”、“平均呼入通话时长”、“部门”、“工号”入搜索框,并在“人工服务接听量”字段后键入“的平均值”,切换图形为散点图,见图7-4-5。
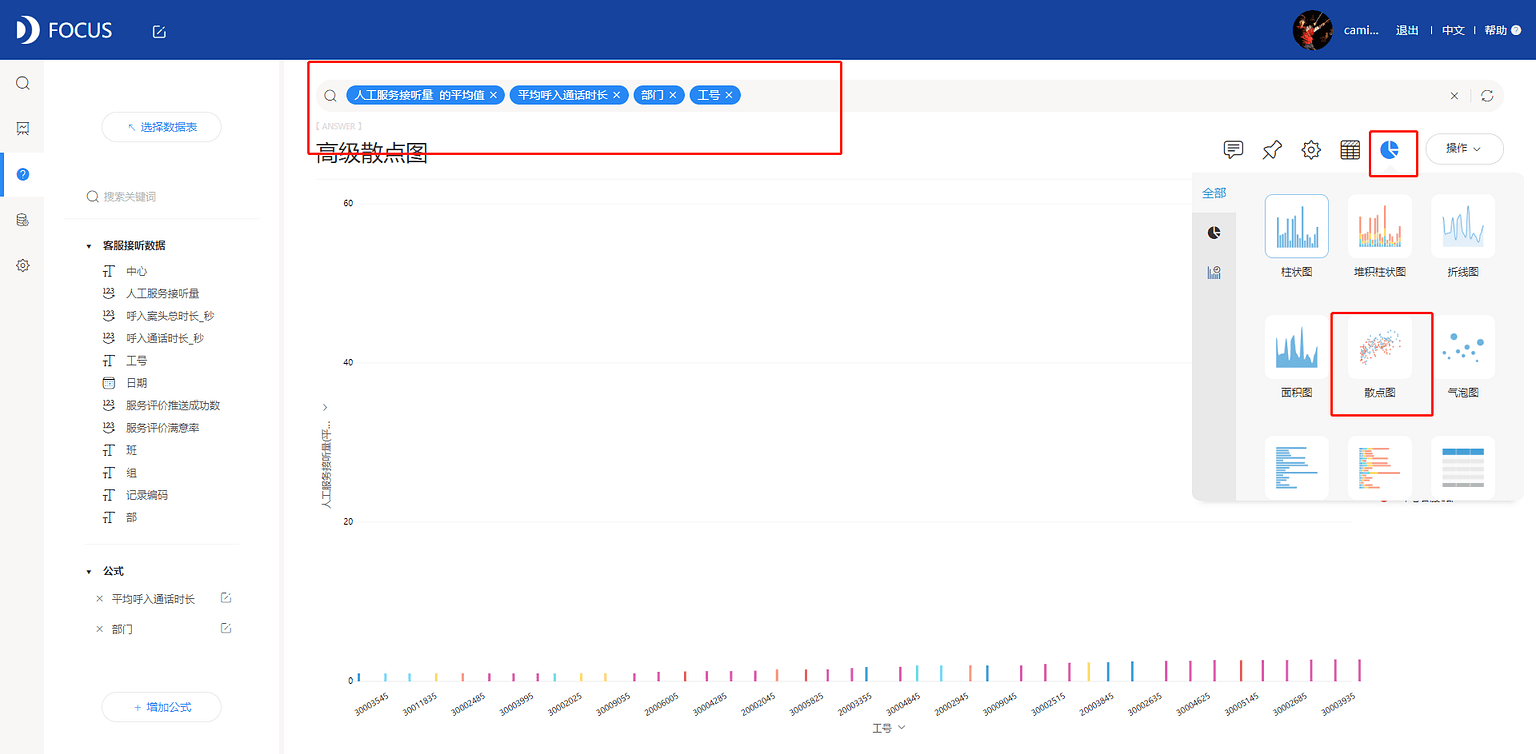
(4)为了更好的查看数据分布,可以设置参考线。设置图表属性——标度,选择平均值,以直线形式呈现,见图7-4-6。
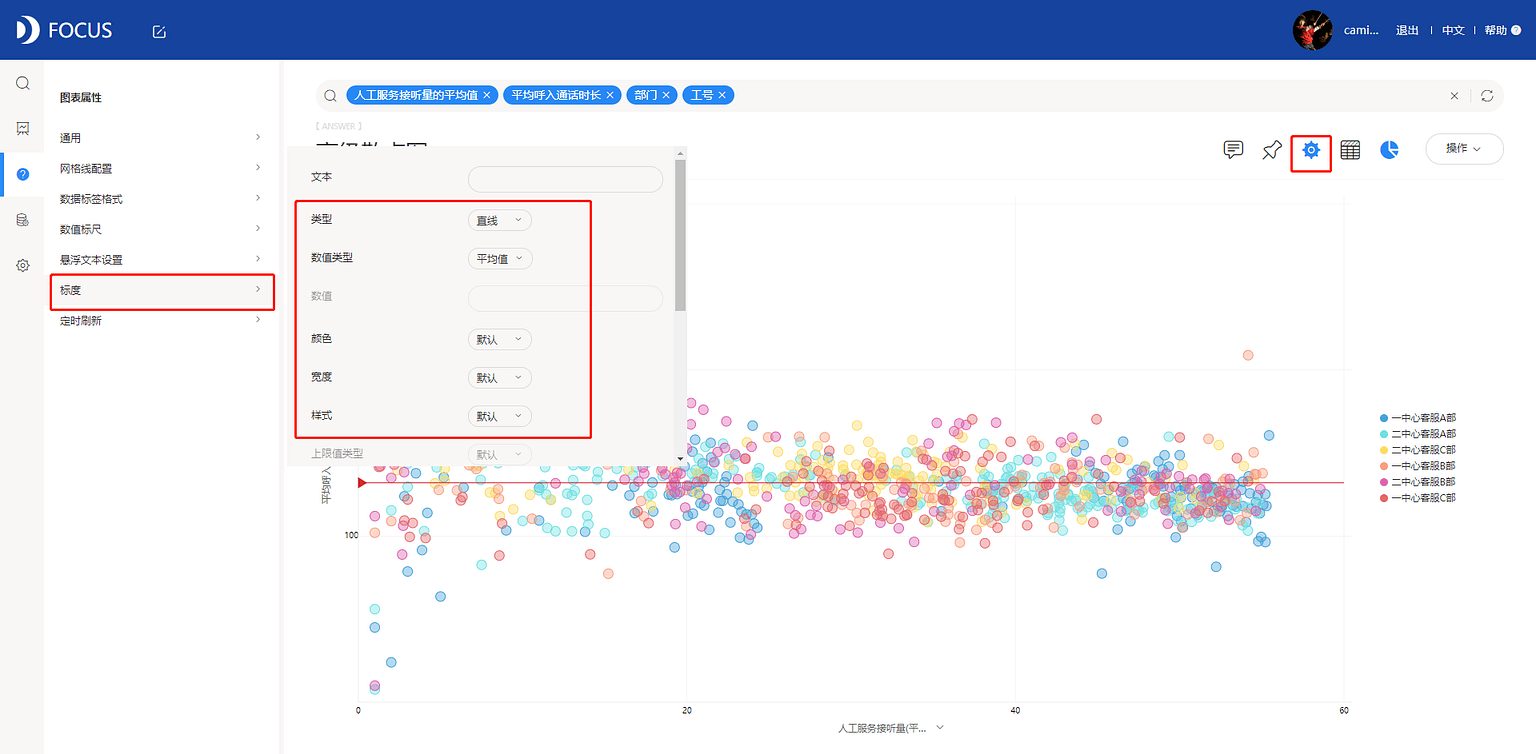
得到高级散点图如图7-4-7所示。从图中可以看出:平均人工服务接听量的数据分布比较分散;平均呼入通话时长大致服从正态分布,大部分客服的平均通话时长集中在100秒——150秒。
7.5 环比同比定基比
在业务分析中,在时间上的业务发展速度是必要的分析指标。一般可分为同比增速、环比增速、定基比增速。增长速度可以是正数,也可以是负数。正数表示增长,负数表示降低。选择合适的图形进行可视化可以一目了然的跟进业务成果,一般比较常用折线图、瀑布图等。本节我们以某零售企业的销售数据为例绘制环比、同比、定基比图,了解它们之间的差异。
7.5.1环比
环比一般指N期水平与N+1期水平或N-1期水平对比,通常分为日环比、周环比、月环比和年环比。下面我们以销售数据为例,计算企业销售金额的月环比。
进入搜索页面,选择“销售数据.csv”数据源,本小节需要用到“订单日期”、“销售金额”字段。 在搜索框中输入“按订单日期计算的销售金额的总和的月增长率”,系统呈现瀑布图。
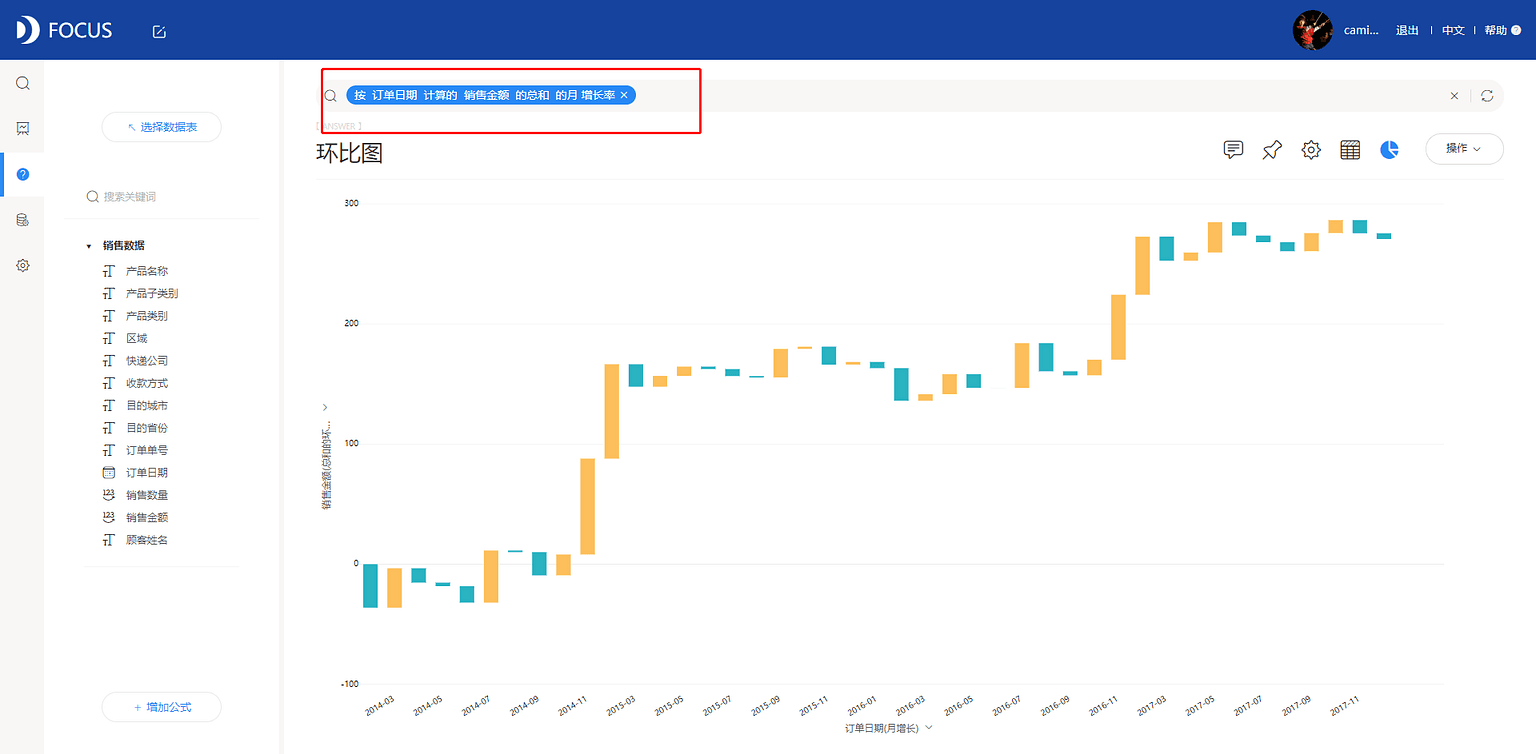
如图7-5-1所示,2014年11月和12月的月增长率较高,而后的月环比处于小幅度波动状态。
7.5.2同比
同比一般指第N年本期发展水平与第N-1年同期发展水平的对比。下面我们以销售数据为例,计算企业销售金额的月同比。
(1)进入搜索页面,选择“销售数据.csv”数据源,本小节需要用到“订单日期”、“销售金额”字段。
(2)在搜索框中输入“按订单日期计算的销售金额的总和的月增长率与往年同期相比”。
(3)切换图形为折线图。
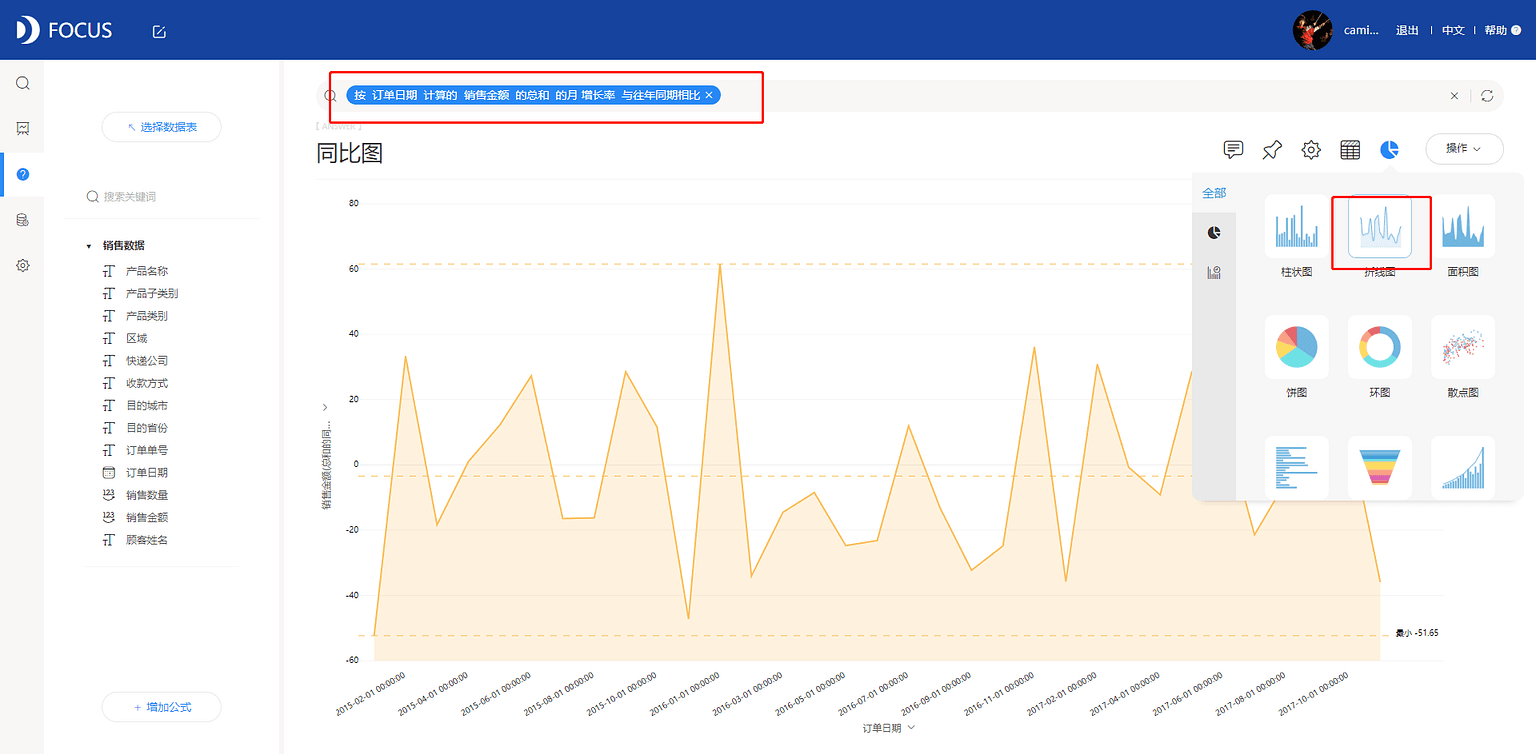
如图7-5-2所示,2015年12月份的同比增速最高,销售额同比亦处于波动状态。
7.5.3定基比
定基增速也称总速度,是报告期与固定基期水平之比,表明在较长时期内该现象的总的发展情况。下面我们以销售数据为例,计算企业销售金额的月定基比。
(1)进入搜索页面,选择“销售数据.csv”数据源,本小节需要用到“订单日期”、“销售金额”字段。
(2)以2014年1月销售金额为对比基准,因此需要得到2014年1月的销售金额总额。在搜索框中输入“2014 一月 销售金额”即可得到,见图7-5-3。
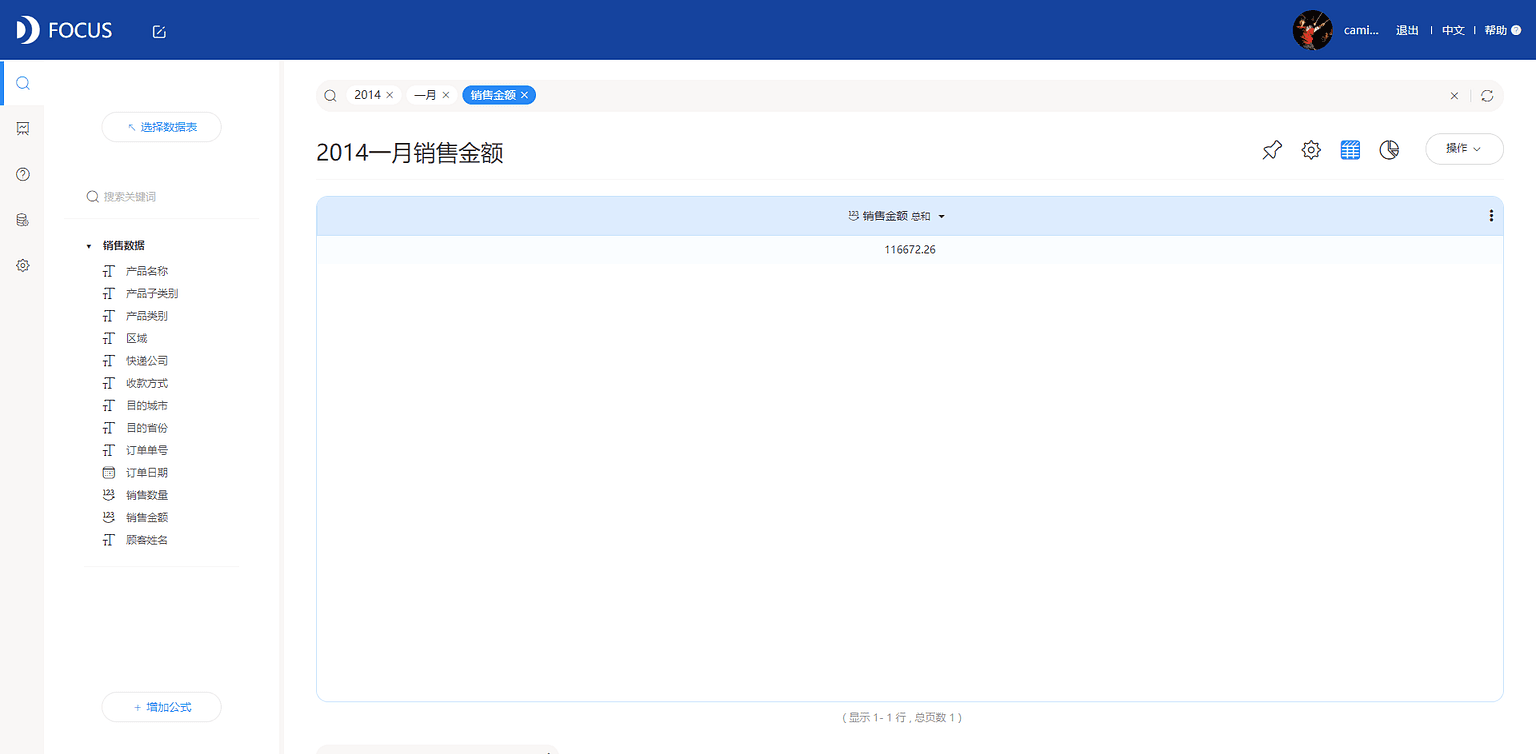
(3)增加“基比”公式字段,见图7-5-4。
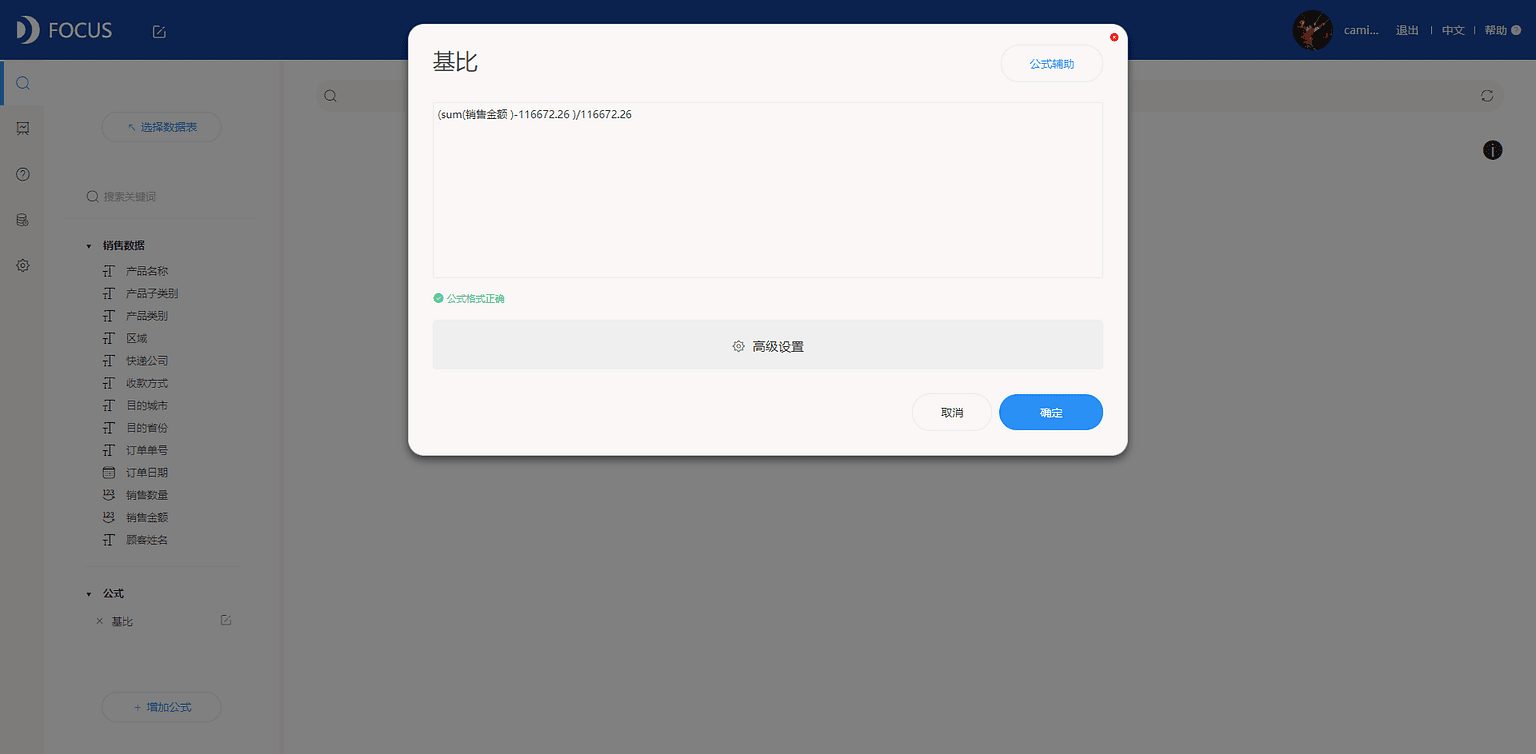
(4)在搜索框中输入“基比 每月”,1月份为基准月,不做视图,因而再筛选订单日期大于等于2014年2月1日,见图7-5-5。
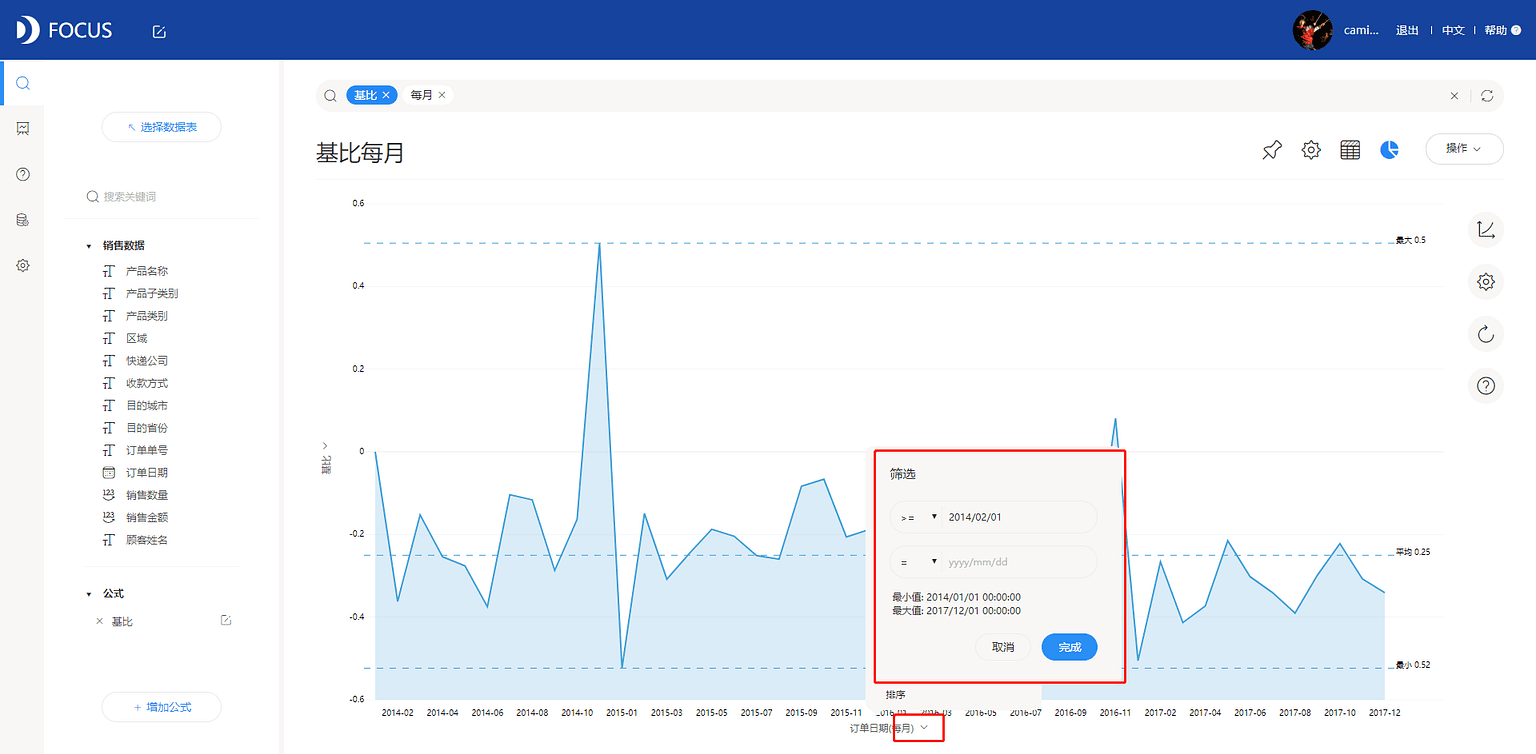
(5)切换图形为面积图,见图7-5-6。
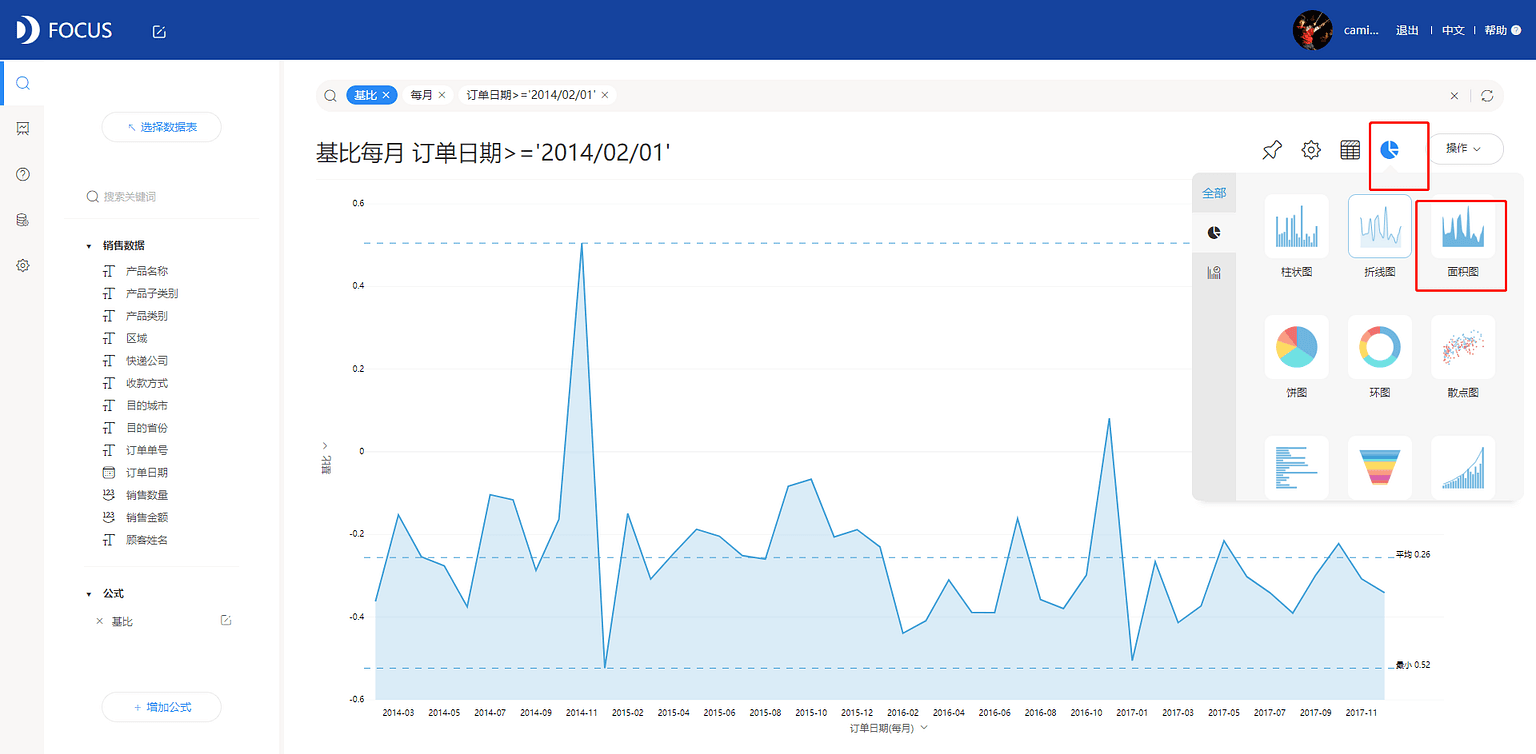
得到最终定基比视图如图7-5-7所示,可以看到除了2014年11月和2016年11月定基比增速为正向,其余均为负向。
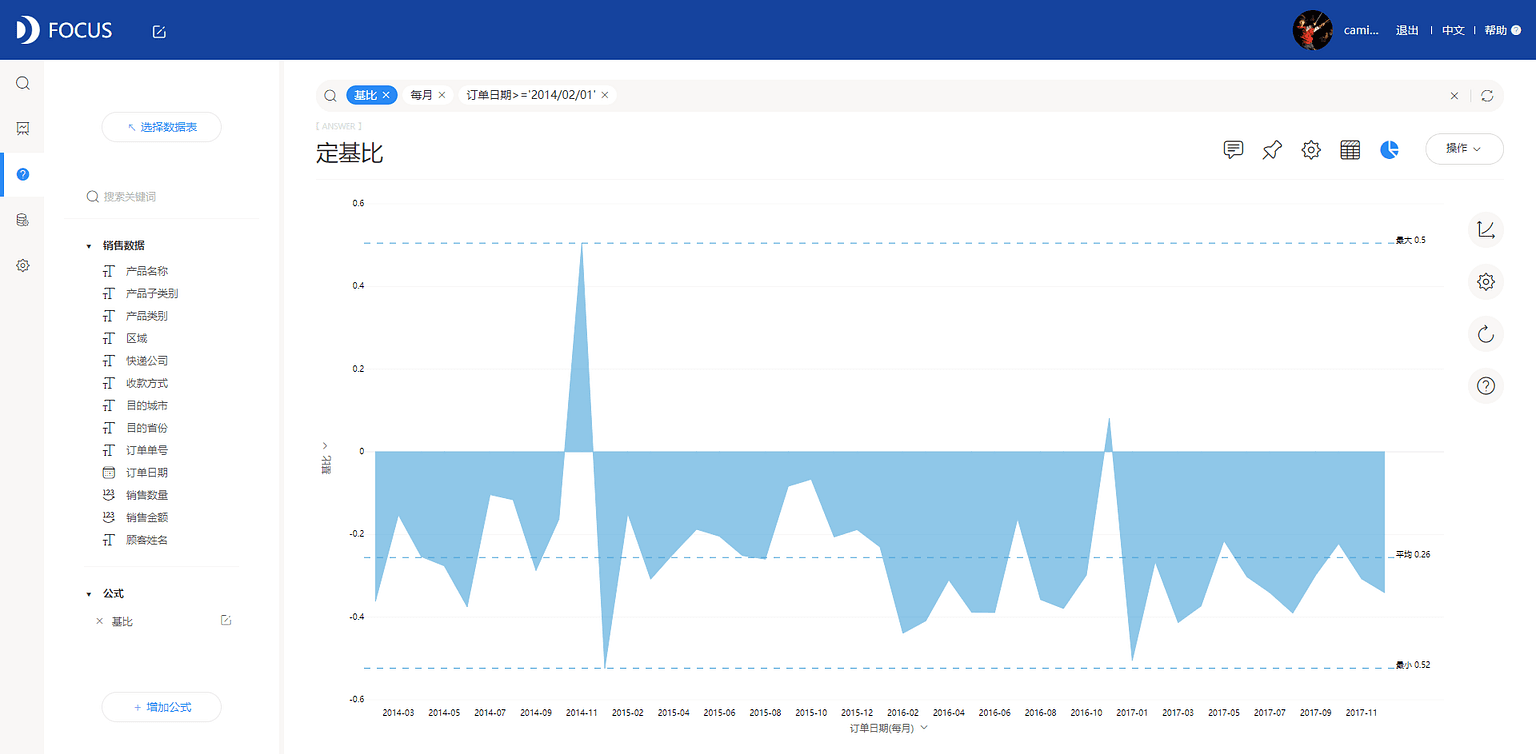
综上,三种增速的比较,最大的区别体现在两个方面。一是对比基数不同,同比的对比基数是上年的同一期间的数据,环比的基数是上一期间的数据,而定基比的基数则是固定的;二是则重点不同,环比侧重反应数据的短期趋势,会受到季节等因素的影响,同比倾向于侧重反映长期的大趋势,规避了季节的因素,而定基比侧重表现现象在较长时期内总的发展速度。